1. Конь вышел с поля а1 и через несколько ходов вернулся на него. Докажите, что он сделала четное число ходов.
2. Может ли конь пройти с поля а1 на поле h8, побывав по дороге на каждом из остальных полей ровно один раз?
3. Фигура «верблюд» ходит по доске 10?10 ходои типа [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image002.gif[/img] (т.е. она сдвигается сначала на соседнее поле, а затем сдвигается еще на три поля в перпендикулярном направлении; конь, например, ходит ходом типа [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image004.gif[/img]). Можно ли пройти ходом «верблюда» с какого-то исходного поля на соседнее с ним?
4. На плоскости проведена сеть линий, в каждом узле которой сходится не более чем 10 из них (узлом называется точка, в которой сходится три или большей линий). Линии раскрашиваются разными красками так, чтобы никакие две соседние линии (линии, сходящиеся в одном узле) не были закрашены одной краской. Доказать, что такую раскраску всегда можно осуществить, если иметь 15 различных красок; однако 14 красок в некоторых случаях уже может не хватить.
Примечание. Раскраска сети линий, подобная той, о которой говорится в задаче, иногда встречается на практике. А именно, в случае сложных электрических цепей для того, чтобы при подключении не спутать провода, удобно пользоваться разноцветными проводами (или проводами, концы которых отмечены разноцветными ленточками); при этом клеммы приборов окрашиваются теми же цветами, что и провода. Разумеется, при этом никакие два привода, подведенных к одному прибору, не должны быть одного цвета. Таким образом, электрические приборы в этом случае играют роль узлов сети нашей задачи, а провода – роль линий сети.
5. Треугольник разбит на более мелкие неперекрывающиеся треугольники так, что любые два из треугольников разбиения или вовсе не имеют общих точек или имеют общую вершину, или имеют общую сторону (т.е. никакие два треугольника разбиения не соприкасаются по части стороны одного из них).
Взвешивания
19 Есть [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image002.gif[/img] одинаковых монет, из которых одна – фальшивая (более легкая). Как с помощью чашечных весов без гирь выделить фальшивую монету за наименьшее число взвешиваний, если а) [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image004.gif[/img]; б) [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image006.gif[/img]; в) [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image008.gif[/img]; г) [img]file:///C:/DOCUME~1/Manager/LOCALS~1/Temp/msohtml1/01/clip_image002.gif[/img] - произвольное число?
20 Перед Вами лежат шесть монет, две из которых фальшивые (фальшивая монета тяжелее настоящей на 0,1 г). Кроме того, у Вас есть чашечные весы без гирь. Весы эти, правда, не очень чувствительные и реагируют на разность грузов не менее 0,2 г. Попробуйте за четыре взвешивания найти обе фальшивые монеты.
21 На суде в качестве вещественного доказательства предъявлено 14 монет. Эксперимент обнаружил, что монеты №№1 – 7 фальшивые, а №№8 – 14 – настоящие. Суд же знает только то, что фальшивые монеты весят одинаково, настоящие монеты весят одинаково, и что фальшивые монеты легче настоящих. У эксперта есть только чашечные весы без гирь.
22 В 10 мешках лежат настоящие монеты, а в 11-м – фальшивые. Все фальшивые монеты весят одинаково и отличаются по массе от настоящих. Имеются точные весы с чашками и стрелкой, без гирь, позволяющих узнать, на какой чашке груз имеет большую массу и насколько. С помощью двух взвешиваний определите, в каком мешке фальшивые монеты.
23 Есть три одинаковые фляги, две из которых пусты, а в третьей налит 1 л молока, цистерна молока и весы без гирь, на которые можно ставить фляги. Как отлить в одну флягу 85 л молока, сделав не более 8 взвешиваний? (Во флягу вмещается больше 85 л. При взвешивании на одну чашку весов ставится фляга с молоком, на другую – пустая и в пустую доливается молоко до равновесия.)
24 Есть гиря общим весом и весы с двумя чашками, находящиеся в равновесии. Вес каждой из гирь выражается натуральным числом. Гири по очереди кладут на чашки весов: сначала самую тяжелую (или одну из самых тяжелых), затем самую тяжелую из оставшихся и т.д. При этом каждую следующую гирю кладут на ту чашку весов, которая в данный момент легче, а если весы находятся в равновесии, то на любую из чашек. Докажите, что после того, как на весах окажутся все гири, весы будут находиться в равновесии.



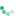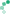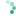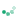
Авторизуйтесь, чтобы оставить комментарий.